Este artículo es una continuación del publicado en este mismo medio en fecha 28 de agosto del año en curso. Conviene pues leer el anterior para mejor entender lo que escribo en este.
Una de las cuestiones mas importantes para utilizar planos y mapas y sacarles provecho es saber manejar sus coordenadas. Los mapas más conocidos por el público en general, son supongo, los que publican tanto el Servicio Geográfico del Ejército como en Instituto Geográfico Nacional (IGN). A ellos me referiré, si bien aclaro que las coordenadas propiamente dichas las llevan a menudo todo tipo de planos. Los de las minas por ejemplo y son esencialmente una herramienta para indicar de modo exacto e inequívoco ( matemático) la posición de un punto. Esto se hace de modo gráfico o de modo exclusivamente numérico, siendo más fácil de visualizar el modo gráfico, pero más exacto el numérico.
Los mapas del Ejército y también los del IGN tienen todos ellos unas líneas rectas que van de arriba abajo y otras rigurosamente perpendiculares. Las primeras señalan “a efectos prácticos” (tener esto muy en cuenta) cual es la dirección Norte-Sur. Las otras señalan por tanto la dirección Este-Oeste. Los mapas en cuestión están hechos tanto a escala 1 a 50.000 como a escala 1 a 25.000. Es lo más habitual. En los primeros por tanto un centímetro del papel son 500 metros o medio kilómetro sobre el terreno. En los segundos sin embargo y lógicamente sólo 250 metros. En los planos a escala 1 a 50.000 las líneas que forman esa rejilla precitada que son rigurosamente paralelas están siempre dibujadas a intervalos de 2 centímetros. En los de escala 1 a 25.000 lo están por el contrario a 4 centímetros. Esto supone que en los mapas a escala 1 a 50.000 cada cuadrado es exactamente un kilometro cuadrado y en los de escala 1 a 25.000 lo mismo, ya que a esta escala 4 centímetros son un kilómetro en el terreno. Esto es exactamente así porque un centímetro multiplicado por 50.000 son 500 metros y sólo 250 si se multiplica por 25.000. Estas líneas que se cortan perpendicularmente es lo que se conoce como las cuadrículas de las coordenadas. Se trata de coordenadas llamadas rectangulares o cartesianas (en honor a un matemático llamados Descartes o Cartesius en latín)
Es esencial saber en que unidades están expresadas las cifras que figuran en la rejilla de coordenadas. En los precitados planos ya hemos dicho que los intervalos o la separación entre líneas es de un kilómetro sobre el terreno. Esto implica que los números que aparecen junto a cada línea vertical (707.426, 707.427, 707.428,…por ejemplo) son kilómetros. Lo mismo ocurre con las líneas horizontales. Por ello si las coordenadas de un punto son por ejemplo X=708.986 ; Y = 4.717.292 hemos de tener muy en cuenta que esos números son los kilómetros que tanto en dirección Este- Oeste ( las X), como en dirección perpendicular(las Y) hay hasta el origen de coordenadas. Es decir a lo que en el caso del artículo anterior (fecha 28 de agosto) sería la esquina de la izquierda y de debajo de la ventana. Estas distancias ya sabemos como hay que medirlas según se explicó en el artículo de fecha 28 de agosto, es decir de modo rigurosamente perpendicular a las líneas que pasan por el origen de coordenadas (la esquina de la ventana precitada).
Es sencillo comprobar que los números van creciendo de izquierda (Oeste) a derecha (Este) en los mapas y asimismo también de abajo (Sur ) hacia arriba (Norte). Ello es así porque el origen de las X se halla hacia el Oeste (más correcto sería decir hacia el Poniente) y el de las Y hacia el Sur.
Los Puntos Cardinales que señalan las cuadrículas se denominan puntos cardinales de las cuadrículas, que no coinciden exactamente con los definidos por una brújula, ni tampoco con los puntos cardinales geográficos. Este es un detalle importantísimo que no obstante a muchos efectos prácticos se puede obviar ya que todos los nortes están relativamente próximos. Los técnicos (topógrafos, geodestas, ingenieros,…) si deben tener esto muy en cuenta. El ciudadano corriente no tanto.
Si nos piden hallar las coordenadas de un punto del mapa donde se cruzan justamente dos de las líneas de la cuadricula el asunto es simple. Sea por ejemplo la línea que pone X= 707.422 que se cruza con la que pone Y= 4.718.220. El punto de coordenadas será lógicamente X= 707.422 Y= 4.718.220 (kilómetros). Ahora bien lo que más a menudo ocurre es que el punto está dentro de una cuadrícula. En este caso resulta evidente que hay que medir las distancias de ese punto a los bordes de la cuadricula en la que se halla y hacerlos siempre de modo perpendicular es decir siguiendo la distancia más corta. Si estuviese justamente en el centro de la cuadricula en cuya esquina de la izquierda y de abajo pone las coordenadas citadas el resultado seria X= 707.422,5 ; Y =4.718.220,5
Sabiendo que el lado de una cuadrícula es un kilómetro o si se quiere 1000 metros hemos de tener cuidado a la hora de indicar el resultado. Si decidimos hacerlo en kilómetros es sencillo. Media cuadricula son 0, 5 km. un cuarto 0,25 Km. y así sucesivamente. La décima parte de una cuadrícula 0,1 km. es decir100 metros. Esta labor implica manejar muy bien el Sistema Métrico Decimal, que nos enseñaban en la escuela y que a menudo era motivo para que el maestro de turno repartiese algún que otro coscorrón porque eso de pasar de metros a milímetros a de centímetros kilómetros a veces era un lio. Para deshacer el lío en mis tiempos de la escuela de la infancia, la vara del maestro andaba siempre al acecho,…pero esto es sólo una anécdota.
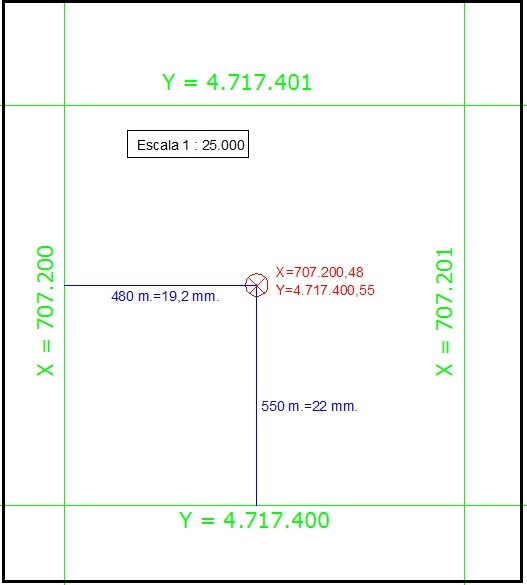
Un buen sistema en este caso (manejo de mapas); es saber lo que supone un milímetro del papel. Un milímetro se mide relativamente bien con una regla. A escala 1 a 50.000 un milímetro son 50 metros y a escala 1 a 25.000 son 25 metros, como debe ser evidente tras lo explicado. Luego al medir sobre el mapa las distancias a los bordes de las cuadrículas resulta muy práctico medirlas en milímetros y luego pasarla a kilómetros. En la figura adjunta se explica. La cuadrícula en la parte izquierda indica 707.200 Km. y en la parte inferior 4.717.400 Km. Medimos (perpendicularmente a la línea de 707.200) sobre el plano una distancia de 19,2 milímetros (hay que afinar mucho para apreciar 0,2 milímetros a simple vista, pero supongamos que lo logramos); que lógicamente a escala 1 a 25.000 son 480 metros o si se quiere 0,48 km. Luego la X vale 707.200 Km. más 480 metros (0,48 km) por tanto ex X= 707.200, 48 Km. o si se quiere 707.200.480 metros. En este caso creo que es mejor hablar en kilómetros,…pero cada cual usa sus métodos.
Lo mismo se hace con la Y. En este caso medimos perpendicularmente a la línea de 4.717.400 Km. una distancia de 22 milímetros. Por tanto (22 x 25.000), son 550 metros. Luego el valor de la Y es 4.717.400 ,mas 0,55 Km. ; es decir 4.717.400,55 Km. Al final todo se reduce a manejar muy bien el Sistema Métrico Decimal ( enseñanza primaria) y a saber lo que es una escala es decir la proporción entre plano y realidad que es también elemental. El tema es que si no hacen muchas practicas se lía uno con frecuencia,….¡¡ me pasa incluso a mi que llevo toda mi vida manejando planos¡¡.
Así pues el que quiera aprender ya sabe como hacer; coger un plano armarse de paciencia, tener a mano una calculadora y ponerse a hallar las coordenadas de cruces de caminos o cualquier otro punto de un plano. Por último aclaro que estoy escribiendo que son labores que como he realizado tantísimas veces; confío en que aunque estoy escribiendo un poco “de carrerilla” no meta la pata en nada. Si así fuese y alguien lo advirtiese le agradecería que me lo dijese. Las equivocaciones son algo tan habitual en la vida humana como dar los buenos días.
Rogelio Meléndez Tercero