Hablar del Antiguo Egipto es hablar de pirámides y es hablar también de geometría. Hace años hallé en la Red (aquí se encuentra de todo) una serie de datos sobre los que con toda lógica cabría llamar los topógrafos egipcios. En alguna parte he leído que los antiguos egipcios debieron aprender geometría o agrimensura debido a la necesidad de saber donde estaban los linderos de las fincas. Estos todos los años quedaban cubiertos por una capa de cierto espesor de limo (barro y arenas) debido a que el Río Nilo se desbordaba inundando los campos cercanos a su cauce.
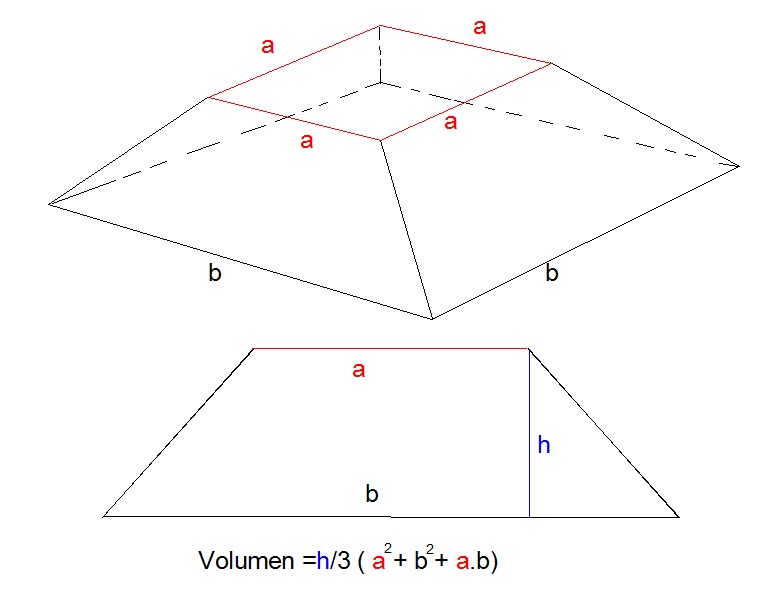
Lo importante y lo que quiero señalar ahora es que me llamó la atención una curiosa fórmula matemática que utilizaban para hallar el volumen de un tronco de pirámide. Ver imagen adjunta . Un tronco de pirámide, es una pirámide a la que se le quita la punta; es decir una pirámide que tiene una base plana lógicamente y una cumbre que es otra superficie plana. En el caso de la figura adjunta tanto la base como la cumbre son dos superficie planas, son cuadrados perfectos y rigurosamente centrados o superpuestos uno encima del otro. La altura entre ambos o diferencia de cota es la distancia h. Ver figura adjunta de nuevo.
La longitud de cada uno de los lados de la base es b y la de la cumbre a. Por tanto la superficie de la base será igual a b multiplicado por b y la de la cumbre será igual a , a , multiplicado por a. Ahora bien ¿Cuál es el volumen de ese tronco de pirámide?.
Recordemos que el volumen de una pirámide es igual al resultado de multiplicar la superficie de su base por la altura y luego dividiendo por tres lo que resulte. Así pues sabiendo la superficie de la base de la pirámide y su altura (dos datos) conoceremos su volumen con facilidad. Ahora bien un troco de pirámide no es una pirámide como es evidente. En este caso los tres datos de que disponemos son la longitud de los lados de la base (b), la longitud de los lados de la cumbre (a) y la diferencia de nivel o la distancia entre las bases (h). Entendemos que en este caso nuestro las bases son cuadrados perfectos y concéntricos es decir que el centro de la base superior o cumbre está justamente en la vertical del centro de la base. Lógicamente las bases han de ser rigurosamente horizontales aunque obviamente no los lados.
Pues bien los antiguos egipcios desarrollaron una fórmula matemática compleja pero rigurosamente exacta. Para hallar el volumen de un tronco de pirámide multiplicaban por si mismo el valor del lado de la una y la otra de las bases y además multiplicaban el lado de una por el de la otra. Es decir, (ver figura) multiplicaban a por a y b por b. También b por a. Así obtenían tres números que después sumaban y el resultado lo multiplicaban por la altura o separación entre las bases . Finalmente el ultimo dato logrado lo dividían por tres y el resultado- según ellos- es exactamente el volumen del tronco de pirámide. Ver figura de nuevo.
Yo comprobé si era correcta esa formula (se precisan unas matemáticas de nivel de enseñanza secundaria) y es totalmente correcta. Si esto es asombroso o no lo dejo al criterio del lector. Si algún estudiante de secundaria lee esto, le recomiendo que para poner a prueba sus conocimientos matemáticos, intente hacerlo; es decir intente demostrar que esa vieja fórmula de los egipcios es correcta. Ya le adelanto que si lo es. Yo personalmente lo he comprobado; pero es que se da además la circunstancia de que este asunto se halla en un antiquísimo papiro que me parece que se encuentra en un Museo de Moscú. Lógicamente habrán sido miles los investigadores que se habrán ocupado de este asunto y que hasta donde yo se coinciden conmigo en que esa fórmula matemática es totalmente correcta.
Para comprobar que esta vieja fórmula egipcia es correcta; yo he partido de la consideración de que el volumen de un tronco de pirámide, es en realidad el resultado de restar el volumen de dos pirámides.
Rogelio Meléndez Tercero