Hace 4 años el jefe de la Agrupación de Voluntarios de Protección Civil del municipio de Castropodame, me pidió que impartiese una clase o algo similar a los miembros de esta agrupación, a la cual yo también me congratulo en pertenecer. Accedí de muy buen grado porque entiendo que es un tema muy interesante, muy útil y que cada vez más se emplea en la vida cotidiana. Por ejemplo para determinar las esquinas de una finca cualquiera en el Registro de la Propiedad o en el Catastro; pero se da la circunstancia de que no es fácil explicar en una o dos horas de que va este tema y por ello opté (después de impartir en efecto una pequeña charla sobre el tema), por escribir artículos sobre este asunto. A la fecha de hoy y sólo con posterioridad al año 2020, he localizado en Internet, 7 artículos escritos por mi y que se hallan a disposición de quien los quiera leer . Pero como aún hay “más cuerda”, aquí van otros más.
Es posible que repita aquí algunas ideas ya expuestas, pero no puedo volver a estudiar uno a uno esos 7 artículos ( incluso alguno o algunos más), supondría “perder” un tiempo injustificado. Intentaré explicar lo que se, del modo más simple posible y en base a conocimientos muy básicos, algunos sacados de las viejas enciclopedias (Alvarez) que se usaban en la escuela del pueblo de Castropodame en los años 60.
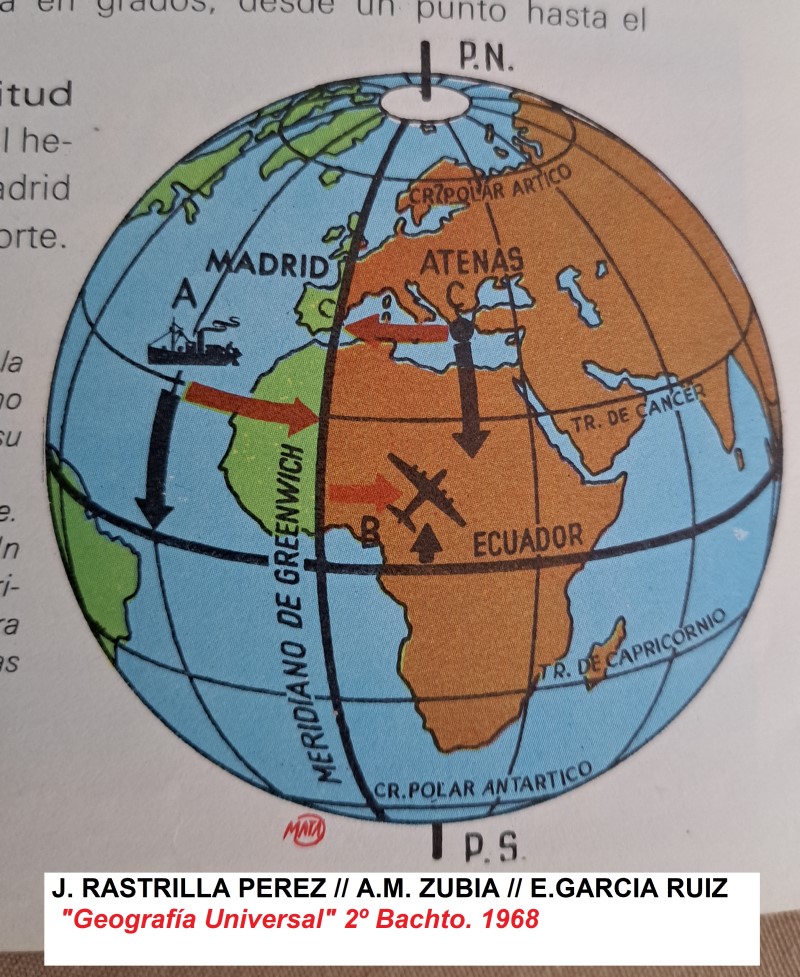
Precisamente en el Parque Solar Didáctico de Castropodame hay un reloj de sol vertical en el que se lee lo siguiente: CASTROPODAME, 42º 35´9” N -6º 27´54” O. Es esta una manera de indicar matemáticamente, la posición de ese reloj o si se quiere la posición de Castropodame en el Mundo. Así estamos diciendo que Castropodame se halla a 42º 35´y 9” al norte del Ecuador y 6º 27´54” al oeste del meridiano de Greenwich. En realidad al poner este dato con signo negativo, no sería preciso señalar que está al oeste del meridiano citado. Hay pequeños detalles que no obstante hay que tener en cuenta. Si esa magnitud fuere al este del meridiano de Greenwich, nos estaríamos refiriendo a un punto que podría corresponder por ejemplo al sureste de Francia. ¡ Vaya despiste! La primera de las cantidades señaladas es lo que se conoce como latitud. La segunda es la longitud, conceptos ambos que también se explicaban en las escuelas de los pueblos en la época de la II República Española. En la enciclopedia de grado medio de J. Dalmau Carles.
Sin embargo en la vida cotidiana y para el ciudadano corriente, lo que más fácilmente se entiende son medidas en kilómetros y no en grados. Solemos hablar por norma general de kilómetros. Hallaremos pues la equivalencia entre grados-minutos- segundos y kilómetros. Para ello vamos a la enciclopedia del pueblo (niños de 8 a 10 años en la época) y una vez visto lo que son los paralelos y meridianos, trataremos de hacer el cálculo. Hemos de aclarar que cada grado tiene 60 minutos y cada minuto 60 segundos. Esto en mis tiempos se aprendía con 12 años. En vez de hablar pues de grados, minutos y segundos vamos a pasar todo a grados a secas. Por ello es obvio que la latitud señalada en ese reloj de sol de Castropodame es de 42,5858333º (grados sexagesimales) y la longitud de 6,465º también grados sexagesimales.
Ahora acudiendo de nuevo a la escuela del pueblo leemos que la Tierra tiene un diámetro de 12700 km aproximadamente. Por ello es evidente que Castropodame ha de hallarse a una distancia de 4719, 72 km es decir redondeado a 4720 kilómetros al norte del Ecuador. Falta por ver la distancia pero en longitud, es decir su posición respecto al meridiano de Greenwich. Aquí el asunto es algo más peliagudo. No se si en la escuela del pueblo se podría hacer. Quizá algún alumno de los más espabilados si. Hay que saber el radio de una circunferencia terrestre que se obtiene “cortando” la tierra por el paralelo situado a 42,5858333º.
Si no sabemos como hacerlo, podemos acudir a dibujar (por ejemplo) una circunferencia de 12,7 centímetros de radio y después medir un radio paralelo al Ecuador y a esa latitud. Yo hice algo muy similar y obtengo un radio de 4700 km. Es un dato de entrada correcto. Sabiendo unas nociones muy básicas de trigonometría y como comprobación se puede rápidamente (en unos segundos), revisar el dato. Yo lo hice con calculadora y obtengo 4675,279 kilómetros. La cosa pinta bien. Ahora ya podemos determinar la longitud en kilómetros. Tomaremos como radio 4675 kilómetros y por ello a una longitud de 6,465º le corresponden 527,5 kilómetros. Luego Castropodame está a 4720 kilómetros al norte del Ecuador (midiendo en dirección norte-sur) y a 527,5 kilómetros al oeste del meridiano de Greenwich midiendo en dirección este-oeste. Con esto ya es suficiente a muchos efectos.
Si medimos en un mapa de España (yo lo he hecho) obtenemos una cifra ya muy cerca a esta. A mi me salen en concreto 524 kilómetros al oeste del meridiano de Greenwich. El mapa de España que utilicé cabe en un papel de 20 x 20 cm. Su escala es de 1 a 4 500 000, es decir un milímetro del papel son 4 kilómetros y medio de terreno.
Hemos logrado por tanto determinar en una primera aproximación la posición de Castropodame en el Mundo. Lo de la aproximación es muy importante. Un error de 5 kilómetros en latitud o longitud puede resultar fatal ya que supondría confundir a Castropodame con Almázcara, Onamio o cualquier otra de las poblaciones vecinas.
En un mapa de África en el que figure también ubicada España se pueden intentar hacer también medidas para comprobar si Castropodame está o no a 4720 kilómetros del Ecuador. Pero hay que andar un poco “avispados”. En mapas que representan grandes superficies en una pared plana, ya se ponen de manifiesto ciertos problemillas porque la superficie de la Tierra, no es plana…pese a lo que dicen los (estúpidos e ignorantes) terraplanistas. La superficie por la que se extiende toda África, es tan enorme que en vez de usar un mapa de los que había en las escuelas del pueblo por ejemplo; hay que usar una esfera y una esfera del tamaño de una rueda de un carro…por lo menos. No abundan esferas del Globo Terrestre tan grandes. Yo tengo una “pequeñica”, es muy similar a las que había en la escuela del pueblo. La medida efectuada por mi sobre esa esfera (diámetro de 25,7 centímetros) me da sin embargo una distancia de 5000 kilómetros. En esa esfera de los colegios un centímetro sobre la misma equivale a 500 kilómetros de terreno. Un pequeño error al medir, “la lía “.
Aquí estamos entrando ya en el terreno de la precisión en las medidas. Asunto muy importante en topografía y que a menudo pasa inadvertido para el público en general. Cuando se realiza una medida, hay que ser muy conscientes del grado de precisión de la misma y si esta es admisible o no. Un error de un centímetro para medir un cristal de una pequeña ventana, puede resultar inadmisible, pero no lo es para medir un campo de fútbol obviamente…ni para determinar la posición de Castropodame en la esfera terrestre de la escuela.
Hemos realizado los cálculos partiendo de datos sólo correctos en una primera aproximación. Hemos además supuesto que la Tierra, es una esfera rigurosamente perfecta, pero sólo lo es a ciertos efectos; por ejemplo para hacer esas esferas terrestres de los colegios. Asimismo es una esfera perfecta, cuando la vemos en fotografías de nuestro planeta realizadas desde el exterior. Aún así hay un pequeño detalle que hemos de tener en cuenta y es que una esfera nunca es una superficie plana. Los mapas y planos de los mares y continentes, de las naciones, de los pueblos y ciudades e incluso de los edificios se han realizado y se realizan desde hace siglos; aparecen en superficies planas por norma general.
Una superficie esférica no se puede convertir en plana. No es desarrollable como si lo es por ejemplo una caja de zapatos o una pirámide o un cilindro. Este es otro problema que hay que solventar, si queremos determinar con rigor la posición de un punto en la superficie terrestre. De momento lo que hemos determinado es la posición de Castropodame en el Mundo con una aproximación correcta a muchos efectos. No a todos. Un error de 5 km por ejemplo, podría ser inadmisible a muchos efectos. Para afinar más y más hay que estudiar el problema más en profundidad. Pues bien… afinaremos pero eso será en el siguiente artículo. Por ahora ya vale.
Rogelio Meléndez Tercero