En las enciclopedias de las escuelas más elementales de nuestros pueblos hace ya muchas décadas, se enseñaban algunos datos sobre las medidas de la Tierra y la Luna y sobre la distancia entre ambos cuerpos celestes. Eran ciertamente cifras válidas a muchos efectos prácticos y que son totalmente aceptables para el conocimiento que debería tener cualquier ciudadano medio. La distancia Tierra-Luna según aquellas viejas enciclopedias es de 385 000 km. El diámetro de la Tierra 12 700 km. y la Luna 50 veces más pequeña que la Tierra. Debía tener yo unos 10 años cuando me enseñaban estas cosas.
No obstante y aunque como una primera aproximación son datos perfectamente aceptables, los aficionados a la astronomía y otras muchos profesionales de campos diversos, saben que estas cifras se pueden precisar y afinar mucho más. La distancia Tierra-Luna oscila entre ciertos límites y asimismo tanto la Tierra como la Luna no son esferas perfectas,…aunque a muchos efectos prácticos podemos considerar que si lo son. No es lo mismo medir la anchura de la Tierra o la Luna en el ecuador que en otras partes.
En cualquier caso y metidos ya en estudios o análisis de cierto nivel podemos considerar que la distancia media entre el centro de la Tierra y el de la Luna son exactamente 384 400 km. También que el radio de la Tierra en el Ecuador es de 6 378,14 km. y que el radio ecuatorial de la Luna es de 1 738,14 km. siendo el radio medio de 1 737,42 es decir prácticamente lo mismo.
El Observatorio Astronómico de Madrid, también llamado Observatorio Astronómico Nacional (OAN) publica año tras año un interesantísimo libro (el Anuario); que muchos aficionados a la astronomía y profesionales de diversos campos (topógrafos o ingenieros por ejemplo), utilizan (utilizamos) a menudo. En este libro aparecen una enorme cantidad de datos numéricos y entre otros muchos (muchísimos más bien), los que me sirven de base para este artículo de divulgación científica a nivel elemental.
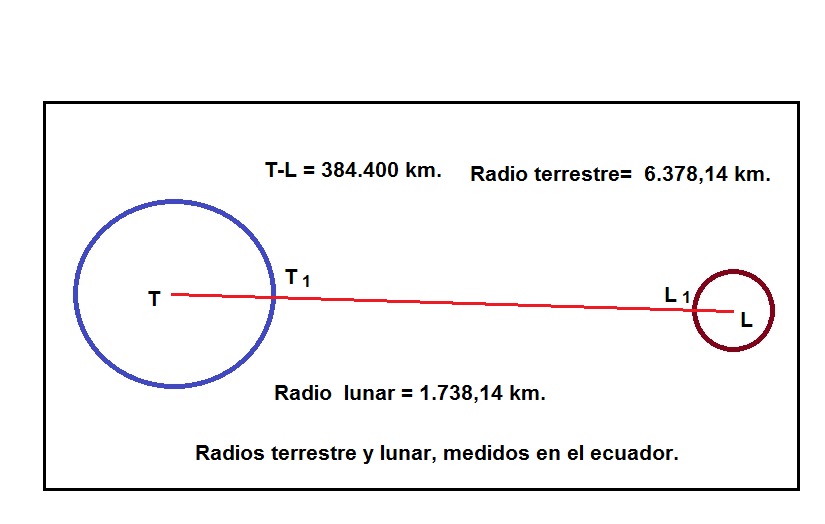
Primero nos fijaremos en el dibujo que acompaña a este artículo, que no está a escala, pero en el que se indican los datos que interesan en este caso. La distancia Tierra-Luna ( T-L de la figura) son los 384 400 Km. ya señalados. El radio de la Tierra que vamos a considerar para unas sencillas operaciones es de 6 378, 14 km. El de la Luna 1 738,14 km.
A partir de estos datos ya podemos empezar a deducir una serie de datos mediante operaciones matemáticas muy simples. Por ejemplo que la distancias T1-L1 será de (384 400-(6 378,14 +1 738,14)) = 376 283,72 km. esta sería la distancia mínima entre dos puntos uno en la superficie terrestre y otro en la superficie lunar, en caso de que la Tierra y la Luna estuviesen exactamente situadas a la que es distancia media entre los centros de ambos cuerpos. En el dibujo se ve perfectamente. Hemos escogido una posición Tierra-Luna singular y asimismo dos puntos singulares (T1 y L1). Si queremos generalizar el cálculo para cualquier otra posición y para diversos puntos, obtendremos ligeras diferencias, pero la filosofía de trabajo utilizada en este caso concreto de este artículo, sirve de punto de partida para otros múltiples casos.
Resulta que hay un aserie de relaciones que se pueden expresar matemáticamente entre la distancia Tierra-Luna y los tamaños de la Luna vista desde la Tierra y viceversa, es decir como se verá nuestro planeta desde la Luna. Para ello hay que considerar que tanto la Luna como la Tierra, no son simples puntos; si no que tienen un cierto tamaño.
Es evidente que la distancia T-L (384 400 km) es 60,286 veces el valor del radio ecuatorial terrestre. Si en vez de considerar la distancia T-L consideramos la distancia T-L1, es decir la distancia del centro de la Tierra a un punto de la superficie lunar alineado con los centros de ambos cuerpos (es decir 382 661,86 km.) resulta que esta será sólo 59,9958 veces el radio ecuatorial terrestre. A partir de este dato es muy sencillo deducir que el radio ecuatorial terrestre desde la superficie lunar y más en concreto desde el punto L1 se verá bajo un ángulo de 0,9549º es decir de 57,2944´ (minutos de arco sexagesimal). Basta dividir 1 entre 59,9958, con lo que obtenemos la cifra de 0,0166678. Unos conocimientos elementales de trigonometría indican que el arco ó el ángulo cuya tangente sea esa cifra será de 57,2944 ´(minutos sexagesimales). Este es un dato importante y se conoce como la paralaje ecuatorial horizontal de la Luna. Otro dato interesante es que el radio ecuatorial lunar es igual al radio ecuatorial terrestre multiplicado por 0,2725, pero este dato no lo vamos a utilizar ahora.
Por otra parte y desde la superficie terrestre y en concreto desde el punto T1,la distancia al centro de la Luna será de (384 400-6 378,14) = 378.021,86. El radio ecuatorial lunar se verá en el punto T1 bajo un ángulo de 0,263443º es decir 15,8066´(minutos). Es el semidiámetro lunar, en el caso que estamos considerando. En realidad estamos haciendo un cálculo similar al efectuado para hallar la paralaje ecuatorial horizontal de la Luna, recurriendo al tema de la tangente de un ángulo concreto.
La relación entre el semidiámetro lunar visto desde la Tierra (SL) y el semidiámetro terrestre (ST) visto desde la Luna, expresados ambos en minutos de arco sexagesimal y en la situación analizada en este artículo, es la siguiente: ST x 0,2758838= SL
En el Anuario del OAN, se señala asimismo que la paralaje ecuatorial horizontal de la Luna, expresada en grados sexagesimales se obtiene de modo muy aproximado dividiendo 57,3 entre la distancia media Tierra-Luna expresada en radios terrestres . En efecto si dividimos 57,3 entre 59,9958 obtenemos la cifra de 0,95507º (grados sexagesimales). Obviamente si queremos saber el valor de la paralaje en minutos hay que multiplicar 57,3 por 60 y dividir el resultado de nuevo por 59,9958. Así obtenemos 57,3´es decir la medida de los 0,95507º (grados sexagesimales); en minutos sexagesimales.
Todo este “baile” de cifras que puede resultar engorroso para el ciudadano medio, es “pan comido” para cualquier astrónomo e incluso para muchos otros profesionales y también para simples personas con ganas de saber.
Señala eso si que en los datos del Anuario hay ligeras y despreciables diferencias con mis datos motivadas me parece por dos motivos. Uno que en el Anuario se hacen cálculos aplicados a cualquier posición de la Tierra respecto a la Luna y a cualquier punto de observación tanto desde la Tierra como desde la Luna. Los puntos T1 y L1 de este artículo son puntos muy singulares. Otro motivo de discrepancias es que incluso en el campo de las matemáticas en función del número de decimales y de otros mínimos detalles se producen resultados que aunque son idénticos a efectos prácticos, son a la vista “distintos”.
Incluso en el campo de la ciencia y de las matemáticas en concreto se producen estas “diferencias”, que para quien no esté muy versado en estos asuntos pueden parecer asombrosas. La cuestión es que en el fondo la verdad total, indiscutible y absoluta hasta en sus últimas consecuencias a veces parece un tanto esquiva y difícil de hallar. Estos deberían saberlo los políticos, sobre todo esos que son tan fanáticos que creen firmemente en que ellos tienen siempre la razón, toda la razón y nada más que la razón y sus oponentes nunca.
Rogelio Meléndez Tercero