Como hace muchos años que regularmente escribo artículos de divulgación científica, a veces me cuesta hallar temas nuevos. Por ello a partir de temas ya analizados y ampliando o matizando ciertos aspectos redacto los artículos actuales.
Pero ¡¡oh sorpresa¡¡ hace poco “buceando” por la Red hallé una serie de noticias sobre un trabajo de geodesia realizado hace ya,…¡¡ unos 1000 años¡¡, por un sabio de nombre Al-Biruni y por lo que veo árabe. Conozco desde mi niñez creo, la célebre medición de Eratóstenes de Cirene (realizada hace más de 2200 años) y que sirvió para determinar la longitud de la circunferencia terrestre, basándose en la diferente inclinación con la que los rayos del Sol inciden en las ciudades de Siena (actual Assuan) y Alejandría. Es cierto que esta medición es aún más antigua que la de Al-Biruni; pero sobre la misma (la de Eratóstenes); yo creo que ya he escrito y hablado hace tiempo así pues ahora toca ocuparse de esta otra medida de la circunferencia terrestre; la que se hizo hace unos 1000 años, como he dicho y que por lo que yo sé es mucho menos conocida.
El autor de esta última vivió en los últimos años del siglo X y primeras décadas del XI. No me voy a ocupar de la vida de este hombre, entre otros motivos porque los datos históricos con el paso del tiempo corren el riesgo de distorsionarse y además se pueden consultar en la Red y en otras partes. Lo que con el paso de los años, los siglos, los milenios e incluso los millones de años permanece inalterable son los razonamientos de índole matemática; como por ejemplo el teorema de Pitágoras. Por ello lo que si se puede hacer, es analizar el razonamiento matemático que según la Historia hizo Al- Biruni para medir la circunferencia terrestre o si se quiere el radio de La Tierra.
Este razonamiento, en base a unos conocimientos de matemáticas relativamente elementales (de enseñanza secundaria) es correcto y consta de dos parte. La primera consiste en medir la altura de una montaña sin subir para nada a la misma. La segunda consiste en subir a la montaña y medir el ángulo bajo el cual se ve el horizonte de la superficie horizontal en la que se asienta la montaña. A partir de la medida de este ángulo y de la altura de la montaña se puede conocer la longitud del radio de La Tierra. La importancia de este nuevo método de medida de la longitud del radio terrestre (y a partir del mismo de la circunferencia) estriba en que parte de observaciones, que nada tienen que ver con las que hizo Eratóstenes; ya que en el método de Al -Biruni no hay que tener en cuenta para nada al Sol ni a las sombras.
DETERMINACION ALTURA DE UN MONTE SIN SUBIR AL MISMO
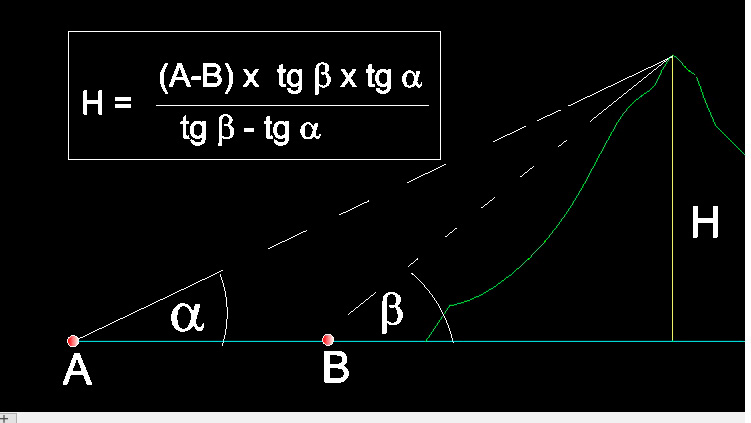
Este método aparece explicado (me parece) en muchos libros de matemáticas de secundaria. Para su aplicación más sencilla es preciso que se trate de un monte rodeado de una zona llana. En la misma trazamos una visual a la cumbre del monte desde un punto A de esa zona llana y anotaremos la pendiente de esa visual. Sean por ejemplo 15º respecto a la horizontal. Luego avanzaremos en rigurosa línea recta hacia la cumbre de la montaña una distancia de por ejemplo y tras avanzar por ejemplo 100 metros volveremos a repetir la operación hecha en el punto A. En este caso la pendiente de la visual será lógicamente mayor, supongamos que son 20º.
Pues bien con sólo estos 3 datos (los 15º, los 100 metros y los 20º) es suficiente para saber la altura del monte. Es un problema de matemáticas muy simple. Pongo la fórmula en la figura. El resultado es que la altura del monte son 101,56 m. La figura no está a escala. Merece la pena estudiarla con mucha atención.
Lógicamente se pueden saber muchos mas datos como por ejemplo la distancia de los puntos A y B a la vertical de donde se halla la cumbre de la montaña; pero ahora este dato no lo precisamos. De este modo logramos saber la altura de la montaña; pero nada más. Nuestro objetivo es medir el radio de circunferencia de La Tierra. ¿Cómo lo podremos hacer?.
MIRANDO DESDE LA CUMBRE DEL MONTE AL HORIZONTE
Si subimos a lo alto de un monte en cuyo repié se extienda una enorme llanura y miramos al horizonte llega un momento en que “el cielo parece tocar el suelo”. Por razones didácticas vamos a suponer que se trata de un monte muy próximo al borde del mar. En Asturias por ejemplo podemos hallar esta situación. La llanura sería en este caso el mar. Ya digo que el ejemplo también valdría para una montaña del interior siempre y cuando la llanura de su base sea lo suficientemente extensa.
En la cumbre del monte al mirar al horizonte por fuerza tenemos que bajar la vista; es decir trazar una visual que nunca será rigurosamente horizontal; aunque eso si muy cercana a la horizontal, tanto que si no utilizamos un instrumento adecuado (un teodolito por ejemplo) o nos las ingeniamos de algún modo, no será fácil medir con rigor suficiente un ángulo tan pequeño. Ahora bien si lo logramos, a continuación y utilizando una formula matemática sencilla y sabiendo la altura del monte podremos determinar la longitud del radio de La Tierra y a partir de este lógicamente la medida de la circunferencia terrestre.
La formula (relativamente simple) en cuestión hay que insertarla con su dibujo correspondiente y explicarla lo mejor posible. Esto lo veremos en la segunda parte. Por hoy vale. El que quiera entretenerse puede ir dándole vueltas al asunto,…..ahora que tenemos tiempo.
Rogelio Meléndez Tercero